降采样

什么是降采样？在时序数据应用场景中，降采样通常是将原始的 N 个数据点，通过某种算法计算，得到 1 个数据点，并在较长周期保存曲线趋势的算法。

降采样带来的好处：

  1. 降低成本。例如将原来的 6 个数据点，降低为 1 个数据点。如此压缩比就是 6:1。而在一些复杂的场景下，6:1 已经是一个很高的比例。
  2. 减少计算。降采后，前端的绘图速度和资源占用也会得到极大的优化。

降采样算法

求平均是一个常见的降采算法，例如我写的一个 demo，就是将 N 个点求平均，得到 1 个新的数据点的实现。

例如原始数据(周期为 10s)为

1
2
3
4
5

[]Point{
    Point{10, 0.5},
    Point{20, 0.3},
    Point{30, 0.4},
}

降采后(周期为 15s)的结果为

1
2
3
4

[]Point{
    Point{10, 0.4},
    Point{25, 0.4},
}

题外话：为什么上述实现的时间戳是向过去时间对齐的？ 主要原因是便于理解，例如当前时间是 21:28:35，在周期是 30s 的情况下，向过去时间对齐的结果是 21:28:30，而向未来时间对齐，结果则是 21:29:00，21:29:00 是未来的时间，很难向用户解释。

那么求平均降采算法的问题是什么？我想放一张图会很直观(以下数据均来自线上生产环境)

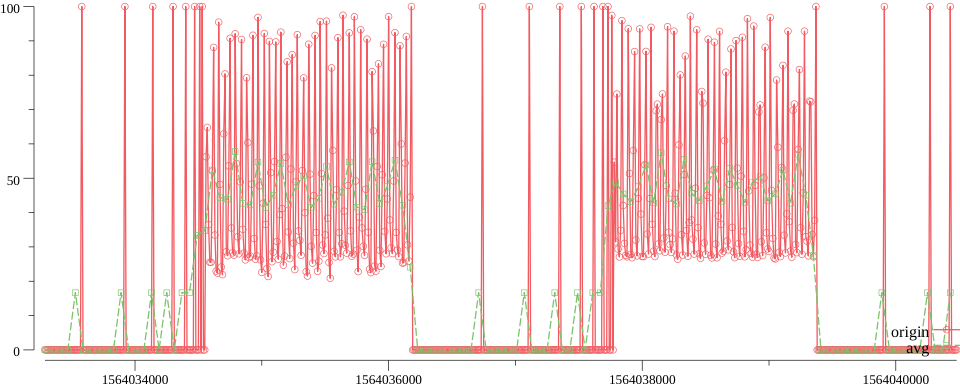
origin vs avg 60s

上图中，将原始曲线的 6 个点，降采为 1 个点。

红色是原始曲线，绿色是经过平均降采算法后的曲线。

可以看出，细节全部丢失。

那么，有没有一种算法，可以兼顾保留细节与达到降采目的的效果呢？

LTTB

LTTB(Largest Triangle Three Buckets) 论文链接

其实一句话就可以概括这个算法的功能：使用较少的数据点，保持原始曲线的视觉特性

那么效果是否如此，看下图：

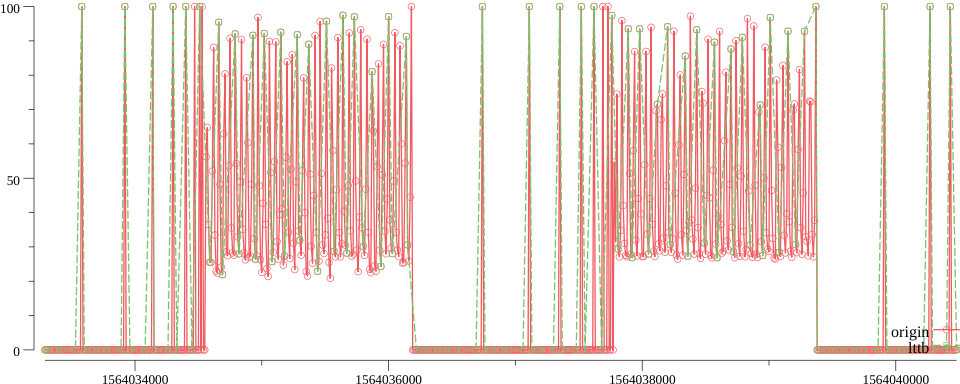
origin vs lttb 60s

上图中，红色是原始曲线，绿色则是经过 LTTB 算法降采后的曲线。

可以看出，细节得以保留。

到这里，效果就已经验证。这个算法是满足我们的需求的。

那么在追求更高压缩比的场景下，LTTB 的表现又如何？

LTTB 在不同 threshold 下的表现

原始 10s -> 降采至 60s

origin vs lttb 60s

  • 压缩比 6:1
  • 绝大部分细节均得以保留

原始 10s -> 降采至 90s

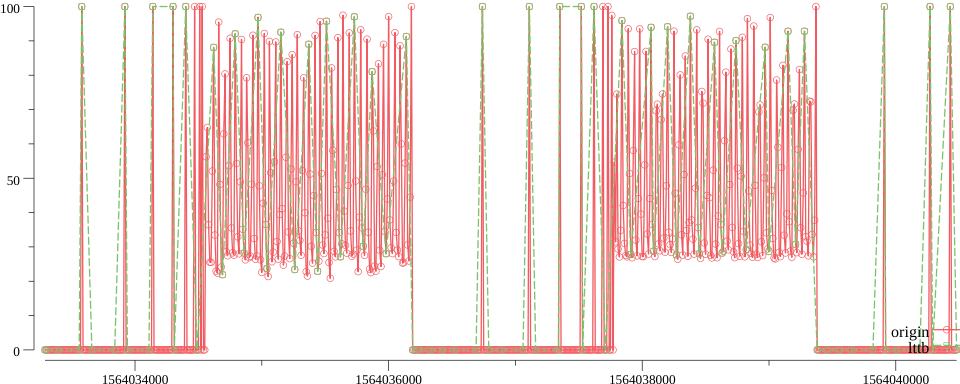
origin vs lttb 90s

  • 压缩比 9:1

原始 10s -> 降采至 180s

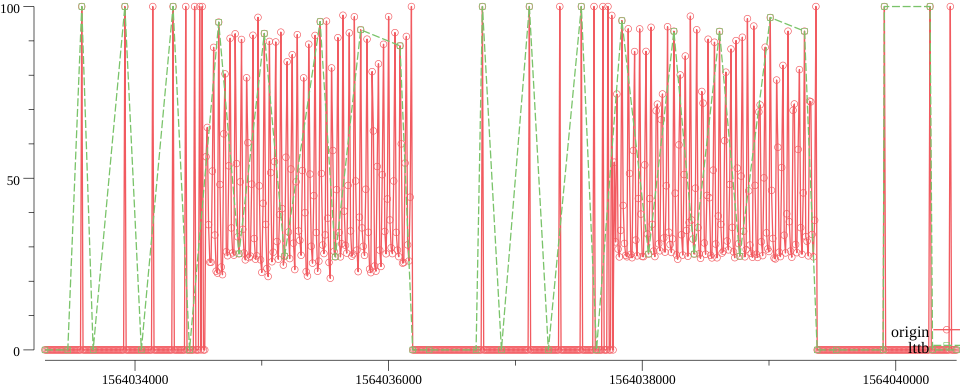
origin vs lttb 180s

  • 压缩比 18:1

原始 10s -> 降采至 300s

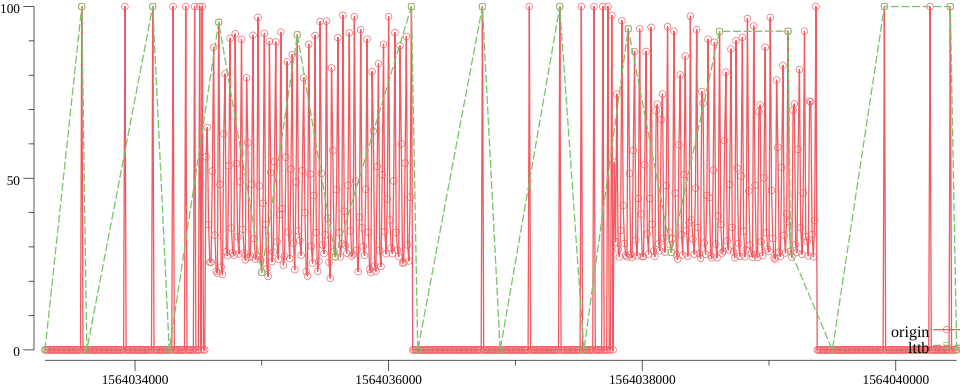
origin vs lttb 300s

  • 压缩比 30:1

在降采至 300s时，虽然很多细节都已丢失。但这时候的平均降采算法又是什么样的？

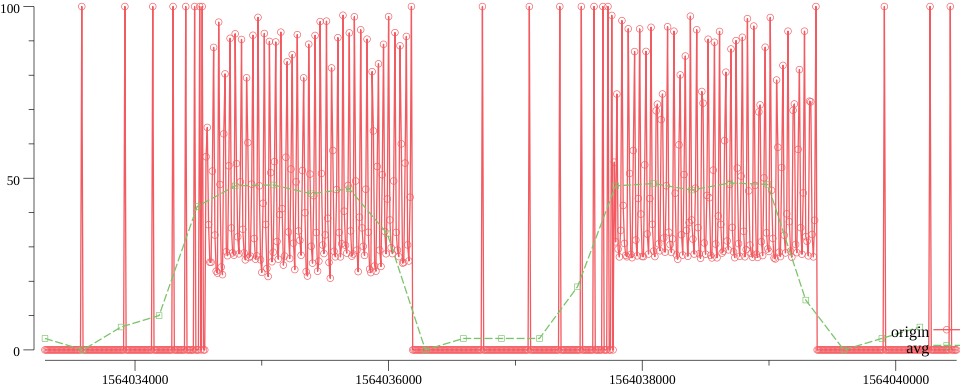
origin vs avg 300s

已经完全看不出原来曲线的样子，只能大概的看出一个趋势。

总结

本文没有什么高深的内容，只是从一个用户的角度，简单的考察一下 LTTB 这个算法，在不同场景下的表现。

总体来说是可以作为生产环境下的降采算法的，比平均降采算法要优秀得多。

附: 相关代码均已放在 github

-EOF-